Vectors

What is a Vector? §

A vector is a “ray” which may be thought of as in space. Or, a list of numbers organized by some property. In machine learning, vectors represent parameters.

%%%A vector can be interpreted in several different ways:

1. Mathematician - Vectors are anything where there is a notion adding two vectors and multiplying vectors by numbers.
2. Physics - Vectors are arrows pointing in space, defined by length & direction. These may be 2D or 3D.
3. Computer Science - Vectors are lists of numbers. These are ordered lists that can be used to represent things such as price and size. %%%

Linear Algebra: §

In Linear Algebra, vectors are simpler. They are 2D arrows from the origin that are defined between an $x$ and $y$ coordinate grid-system. arrows pointing in space.

When a vector is multiplied by some multiplicand, such as 1/2, 2, -1.8, that is referred to as “Scaling”, and the multiplicand is called a “Scalar”.

Cross product (Vector Product)

Components of Vectors §

Vectors have components. Components are x and y coordinates that “compose” the vector. An example of this is a vector (8, 13). This indicates we go out +8 in the x-axis, and +13 in the y-axis.

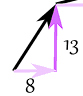
It is often that our problem will provide us with a magnitude and angle for the vector, and we must find the components ourselves. Keep in mind that when provided with a magnitude ($r$) and angle ($\theta$), we are presented the vector in Polar Coordinates.

We may convert from Polar to Cartesian to discover the components. This conversion can be completed as so:

$x=r\ast cos(\theta )$ $y=r\ast sin(\theta )$

Vector addition §

Vector addition is a useful operation for applications such as determining the Net Force of an object.

For one-dimensional vectors that exist only on the x or y plane (and not both) … TODO:

For two-dimensional vectors, we must separate the vector into its components to find the resultant vector’s ($R$) components.

$A_x+B_x=R_x$ $A_y+B_y=R_y$

and by leveraging trigonometric properties we may convert the resultant from component form to it’s pure form: $\sqrt{R_x^2+R_y^2}=R$

Tip

$R$ in the equation above may also be thought of as the magnitude.

$ta{n}^{-1}(\frac{R_y}{R_x})=\theta$

For problems where we are given a vector in it’s pure form (only magnitude ($R$), and direction ($\theta$)) we may convert it to component form by leveraging the following properties of trigonometric functions: $cos(\theta )=\frac{x}{r}sin(\theta )=\frac{y}{r}$ thus, rearranging the above equations result in: $rcos(\theta )=xrsin(\theta )=y$

Vector subtraction §

$d=a-b=a+(-b)$

Vector multiplication §

$f=s\ast a$

#sapling