Simultaneous Localization and Mapping (SLAM)

Why SLAM? §

Lidar is accurate but there is a large degree of uncertainty in the Odometry.

Considerations when using SLAM Algorithms: §

1. Uncertainty of the system’s state: Using a suitable probabilistic representation of the state of the system to represent uncertainty (i.e a mathematically rigorous method)
2. Bayesian Inference: we may use Bayesian Inference to estimate the state of the system.
3. Choice of appropriate measurement models w.r.t measurements representation digitally and the trade-offs made in their design.
4. Runtimes & Efficiency: SLAM algorithms may be computationally intensive. Mathematical foundations and computational tradeoffs are an important focus during design.
5. Potential of implementing AI techniques: deep learning and reinforcement learning may improve performance and accuracy.

Key Challenges: §

State Estimation §

Uncertainty w.r.t Sensors §

LIDAR sensors and cameras are subject to measurement noise. This introduces uncertainty into the state of the system. Additionally, dynamic environmental factors such as weather, lighting, and edge-cases can impact the accuracy of sensors.

Techniques for State Estimation: §

Bayes’ Theorem §

$p(a|b)=\frac{p(b|a)p(a)}{p(b)}$

• where $P(A|B)$ is the posterior probability of event A given event B
• where $P(B|A)$ is the likelihood of observing event B given event A
• $P(A)$ is the prior probability of event A
• $P(B)$ is the marginal likelihood or probability of observing event B

This is to say that our belief about the probability of an event A given new information B is proportional to our prior belief about the probability of A multiplied by the likelihood of observing B given A.

Bayesian Inference allows us to incorporate prior knowledge about the state of the system into the estimation process. Further, with Bayes’ Theorem, we may estimate the state of the system and the map, given noisy sensor measurements and prior knowledge about the system.

Example

$P(\text{disease | positive test})=P(\text{positive test | disease})\ast P(disease)/P(positivetest)$

where $P(\text{positive test | diseas}e)$ is the likelihood of a positive test result given that the person has the disease (0.95), $P(disease)$ is the prior probability of having the disease (0.01), and P(positive test) is the marginal likelihood of a positive test result, which can be calculated as follows:

$P(\text{positive test})=P(\text{positive test | disease})\ast P(disease)+P(positivetest|nodisease)\ast P(nodisease)$

where $P(\text{positive test | no disease})$ is the probability of a positive test result given that the person does not have the disease $(1-0.99=0.01)$, and $P(\text{no disease})$ is the prior probability of not having the disease $(1-0.01=0.99)$

Plugging in the values, we get:

$P(\text{positive test})=0.95\ast 0.01+0.01\ast 0.99=0.0694$

So, the final result is:

$P(disease|\text{ positive test})=\frac{0.95\ast 0.01}{0.0694=0.1359}$

This means that the posterior probability of having the disease given a positive test result is 0.1359, which is much higher than the prior probability of 0.01, but still relatively low. This suggests that the test result is not very conclusive, and further tests and observations are needed to make a definitive diagnosis.

Filtering Algorithms §

Filtering algorithms are used for estimating the state of a system in the presence of uncertain information.

Examples of filtering algorithms include:

• Extended Kalman Filter
  • More efficient than PF.
  • Good for a system which may be modeled as non-linear but continuous.
  • Particular useful for real-time application
  • Requires more assumptions than PF (linearity, Gaussianity, measurement noise)
• Particle Filter
  • Highly Flexible.
  • Supports non-linear and non-Gaussian systems.
  • Well-suited for multi-dimensional systems and non-Gaussian distribution of states.
  • Implementation is feasible (not overly complex)
  • Can be used with minimal assumptions about the underlying system.

Particle Filter §

AKA ‘Monte Carlo Filter’ is a probabilistic algorithm for state estimation. The state of the system is represented as a set of particles each with a weight that represents the likelihood of that particle being the true state of the system. A Bayesian approach is used to update weights based on measurements and a motion model.

Info

Particle Filter Algorithm

- Randomly sample particles from the current state distribution. §

- Use Motion model to predict their future locations. §

- Update their weights based on the measurement likelihood. §

- Particles with higher weights are more likely to be true state. §

- Return weighted mean of the particles as the estimated state §

Quick-N-Dirty Particle Filter Code Implementation: §

# particles = set of particles that represent the state of system. 
 
# weights = represents likelihood of each particle being true state
 
# measurement = latest measurement of the system 
 
# motion_model = blackbox function to predict next state of particles
 
# measurement_model = blackbox function for computing measurement likelihood for each particle.
 
import numpy as np
import random
 
def particle_filter(particles, weights, measurement, motion_model, measurement_model):
    # Predict the next state of the particles
    particles = np.array([motion_model(p) for p in particles])
    
    # Compute the measurement likelihood for each particle
    weights = np.array([measurement_model(p, measurement) for p in particles])
    
    # Normalize the weights
    weights /= sum(weights)
    
    # Resample the particles based on the weights
    new_particles = np.zeros(particles.shape)
    idx = np.random.choice(len(particles), size=len(particles), p=weights)
    for i, j in enumerate(idx):
        new_particles[i, :] = particles[j, :]
    
    return new_particles

Extended Kalman Filter §

EKF is a linearization-based algorithm for state estimation. It is an extension of the classical Kalman Filter and is useful when inputs & outputs cannot be described by a simple linear equation.

EKF works around the non-linear nature of the system by linearizing the model at each time step and then applying the Kalman Filter to the linearized model. From the linearized model predictions may be made and then may be compared to the actual measurements to compute the Kalman Gain and update the estimated state. This process is repeated over time to estimate the state of the system in real-time.

Note

Kalman gain is the weight given to measurements and current-state estimate. High gain means filter places more weight on most recent measurements and conforms to them more reponsively.

Info

EKF Algorithm Generalized

1. Initialize state estimate and state covariance matrix based on prior knowledge of the system. §

2. Linearize the non-linear measurement model §

3. Predict the state estimate and the state covariance matrix based on the control input and the state transition model. §

4. Compute the measurement residual and the Kalman gain. §

5. Update the state estimate and the state covariance matrix based ont eh measurement residual and the Kalman gain. §

6. Repeat steps 3-5 for each measurement. §

###### Quick-N-Dirty EKF Code Implementation: 
```python
import numpy as np

def prediction(x, P, F, Q):
    x = np.dot(F, x)
    P = np.dot(F, np.dot(P, F.T)) + Q
    return x, P

def measurement_update(x, P, z, H, R):
    y = z - np.dot(H, x)
    S = np.dot(H, np.dot(P, H.T)) + R
    K = np.dot(P, np.dot(H.T, np.linalg.inv(S)))
    x = x + np.dot(K, y)
    P = P - np.dot(K, np.dot(H, P))
    return x, P

def ekf(z, u, x, P, F, H, Q, R):
    x, P = prediction(x, P, F, Q)
    x, P = measurement_update(x, P, z, H, R)
    return x, P

Smoothing Algorithms §

• E.g: Pose Graph Optimization

Full trajectories are estimated from complete set of measurements.

Pose Graph Optimization §

The general idea is to represent the mapping and localization information as a graph of positions and orientations and then create constraints between those poses.

Through optimization, we minimize errors in the constraints and achieve a globally consistent estimate of the poses and the surroundings. This may be visualized as a type of “tension” created between nodes (poses) and the distance they have from their measured points.

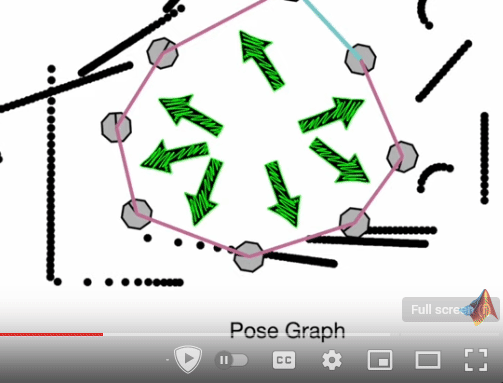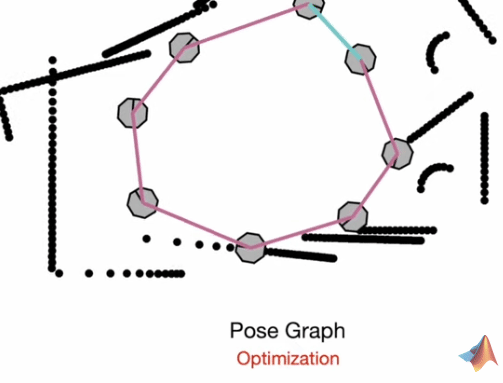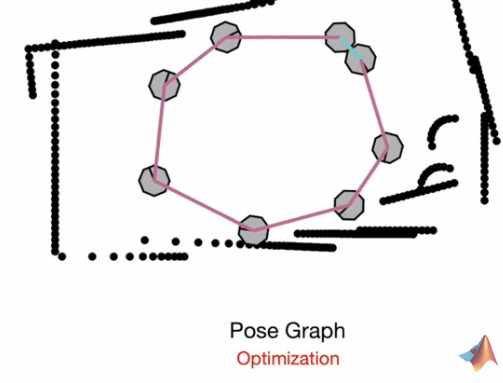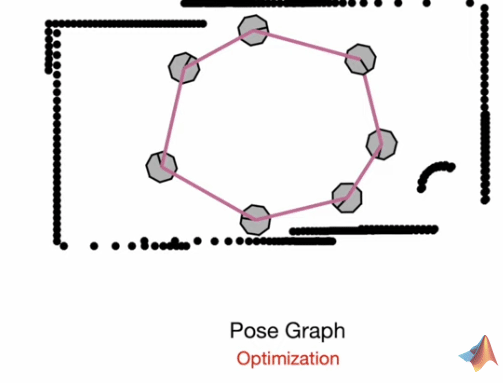
Feature-detection paired with SLAM for higher prediction accuracy §

Achieving high model accuracy when working with small datasets in machine learning can be a challenge.

Techniques for improving model accuracy & efficiency §

Feature Engineering §

Better suit data to the problem to produce new features for both supervised and unsupervised learning, with the goal of simplifying and speeding up data transformations while also enhancing model accuracy.

Regularization §

Regularization is a regression technique to avoid overfitting. Overfitting is what occurs when your model is valuing noise in the training dataset. Regularization regularizes the coefficient estimate towards zero. $Y\approx \beta 0+\beta 1X1+\beta 2X2+\dots +\beta pXp$

Cross-validation §

Cross-validation is another technique to avoid overfitting. Helps estimating the error over test set and deciding what parameters work for the model.

Ensemble Methods §

Transfer Learning §

Data Augmentation §

Quantization §

Quantization is the process of converting a continuous signal or continuous set of values into a finite set of discrete values.

Quantization Resolution §

In Quantization, a continuous signal is divided into a number of discrete levels. The number of levels used determines the quantization resolution - which is directly related to the accuracy of the quantized signal.

A higher number of levels results in a more accurate quantized signals at the cost of storage and computational resources.

In image processing, quantization is used to reduce the amount of data required to represent the signal, while still preserving its essential features.

Quantization is effective at improving efficiency but comes with important implications for the quality of the processed signal. The quantization error, which is the difference between the original continuous signal and the quantized signal, can cause distortion in the processed signal.

Source(s): §

• Bayesian Approaches to Localization, Mapping, and SLAM
• Understanding SLAM using Pose-Graph Optimization
• Feature Engineering Techniques
• Regularization Technique

#evergreen