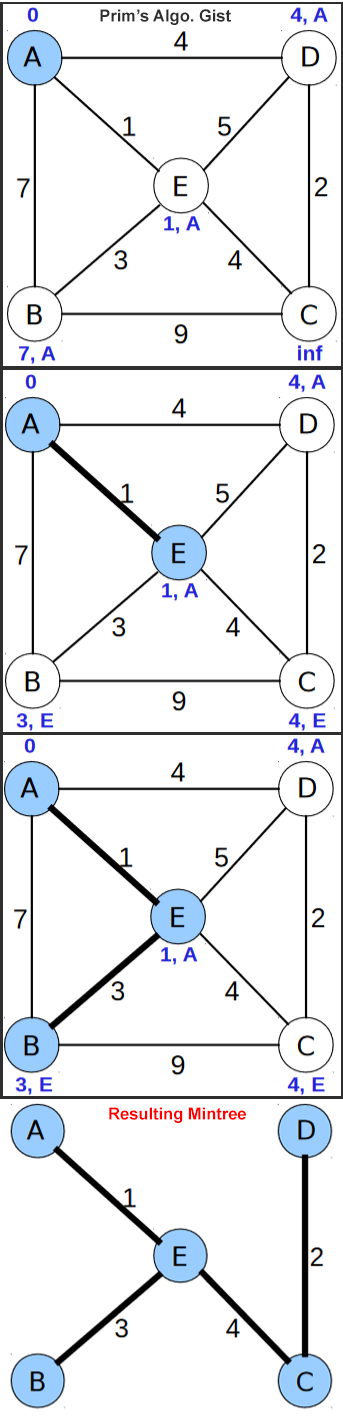
Prim’s Algorithm
Prim’s Algorithm results in a Minimum Spanning Tree, a min-weight connected graph with no cycles.
Algorithm Summary:
- Select a start vertex and initialize it to zero, all other vertices will be initialized to infinity. This starting vertex automatically will become a part of the MST we are constructing.
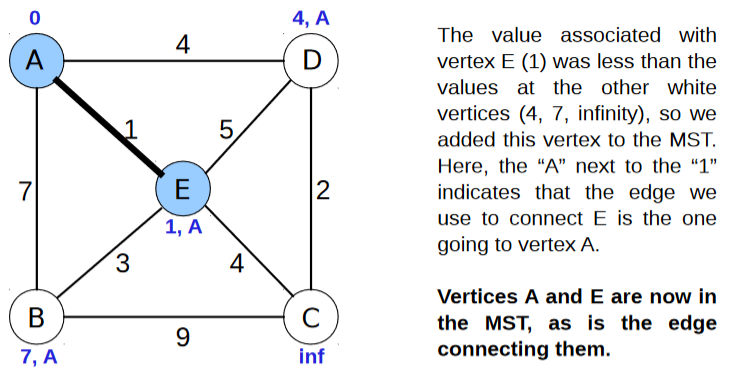
- If the edge weight of our start vertex to the adjacent vertices is less than the value already assigned to that vertex then update the value accordingly. We also track the source node that gets us to this node at that cost.
- Once we have completed the above step for all adjacent nodes to our start node, we now consider all vertices, and pick the one with the lowest cost and add it to the MST with the edge that got us there.
- We then update the values at vertices adjacent to the new vertex (excluding vertices already within the MST) only if the cost of travelling from this new vertex to that adjacent is smaller than the current value assigned to that vertex.
Runtime:
Create empty list called visited[] Select an arbitrary node. We’ll select A. Algorithm will begin from this node. Add a to visited. Next, check all adjacent nodes.