Dijkstra’s algorithm
Dijkstra’s algorithm is a Single Source Shortest Path (SSSP) algorithm for graphs with non-negative edge weights. SSSP means that we need to specify a starting node for the algorithm. Once we provide this starting node, Dijkstra’s can tell us the lowest-cost path between the start node and all other nodes in the graph.
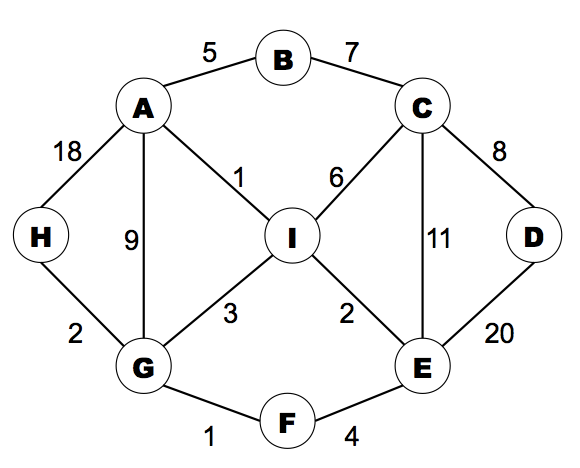
It is important to note that, in referring to shortest paths in this context, we are referring to the sum of the edge weights along each path — not the number of edges in each path. Thus, in the above diagram, the shortest path from A to H is not A → H (with a cost of 18). Rather, it is A → I → G → H (with a total cost of 6).
Constraints / Prerequisites:
All edges of the graph need to have a non-negative edge weight.
Algorithm Summary:
- Maintain a ‘dist’ array where the distance of every node is initialized at positive infinity. Mark the distance to the start node ‘s’ to be 0.
- Maintain a PQ of key-value pairs of (node index, distance) pairs which tell you which node to visit next based on sorted min value.
- Insert (s, 0) into the PQ and loop while PQ is not empty pulling out the next most promising (node index, distance) pair.
- Iterate over all edges outwards from the current node and relax each edge appending a new (node index, distance) key-value pair to the PQ for every relaxation.
Lazy Implementation:
WIP
Eager Implementation:
WIP
Time Complexity:
Depending on the implementation, the runtime is O(), fairly competitive vs other shortest path algorithms.