What?
Semantic Segmentation is the idea of colorizing a category (such as a person) as a specific color.
Hierarchal semantic segmentation explains visual scenes with multi-level abstraction. So instead of labelling all persons as simply “person” HSS attempts to consider structured class relations such as indicating a man with a bicycle as a “rider”.
Why?
The inspiration for doing this is to understand this world over
multiple levels of abstraction, in order to maintain stable,
coherent percepts in the face of complex visual inputs
How?
The paper proposes a novel approach for hierarchal semantic segmentation. Classes are organized as a tree, allowing for the observations to be associated with their ‘root-to-leaf’ route (in similar fashion to how Tries work). E.g: Human -> Rider -> Bicyclist. This structure of class hierarchy further benefits the training algorithm by enforcing constraints by nature of the structure. They call predictions which adhere to the structure of the hiearchy as “hierarchy-coherent predictions” and claim that the technique further yields to more efficient training by allowing their model to consider the criticality of prediction mistakes: which is important for applications such as self-driving where the model may confuse pedestrian with lamppost.
Technical Details
HSS is formulated as a pixel-wise multi-label classification task
Implementation Example:
HSSN Pytorch is an implementation of Deep Hierarchal Segmentation. It is implemented by extending MMSegmentation, a semantic segmentation toolbox based in PyTorch. This toolbox consists of 20 Computer-vision related projects: allowing for 3D Human parametric models, compression, learning, text-detection, as well as additional image and video related tools and benchmarks.
What does each Equation mean?
Eq. 1
Optimized Categorical Cross-entropy Loss
This function is used for Multi-class classifications. An encoder is used to map an image into a dense feature tensor. Then using softmax function we get a score map . This is stored in a score vector and used in combination with ground truth leaf label set .
Eq. 2
Optimized Binary Cross-entropy Loss
s = augmented score map V = the entire class hierarchy = groundtruth binary label set
Eq. 3
Top-scoring root to leaf path where denotes a feasible root-to-leaf path.
Eq. 4
Tree-Min Loss, Hierarchy-coherent score map
Eq. 5
Hierarchal Segmentation Training Objective (tree-min loss) which replaces Binary Cross Entropy in Eq. 2
%%% WIP %%%
Eq. 6
Focal Tree-Min Loss
This adds a modulating factor to the tree-min loss equation from Eq. 5 so as to reduce relative loss for well-classified pixel samples and focus on difficult ones.
Eq. 7
Tree-Triplet Loss where our i values are embeddings obtained from the encoder and bracketed values denote a distance-function used to measure similarity between two inputs, shown:
Eq. 8
Separation Margin: forces the gap of bracketed pairs larger. When the gap is larger than margin the loss value would be zero.
: = 0.1 and is a constant for the tolerance of intra-class variance.
%%% WIP %%%
What does each Figure Mean?
Figure 1:
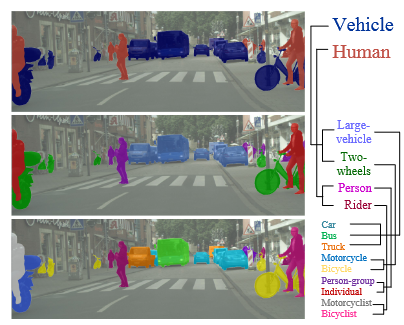This figure simply attempts to illustrate the Hierarchal structure of the taxonomy of objects within a scene. This taxonomy was originally defined in a paper The Mapillary Vistas Dataset for Semantic Understanding of Street Scenes
Figure 2:
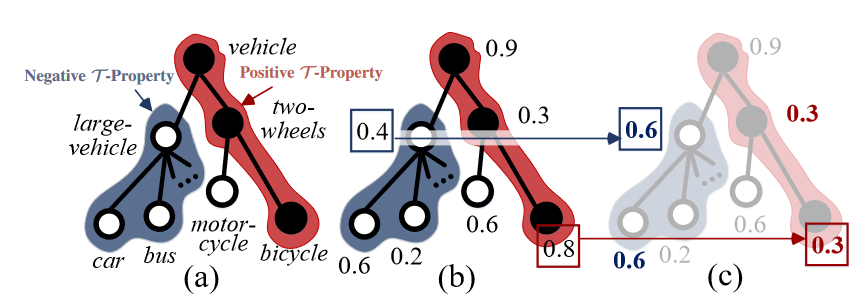This figure illustrates the data structure used to enforce hierarchy constraints. This data structure is a colored tree, where colors represent positive (red) or negative (blue) t-properties. This property is important for Pixel-Wise Hierarchal Segmentation Learning. For each pixel, a positive t-property indicates that all ancestor nodes (i.e superclasses) are also labelled positive. A negative t-property indicates that all child nodes (i.e subclasses) in T should be labeled negative.
Figure 3:
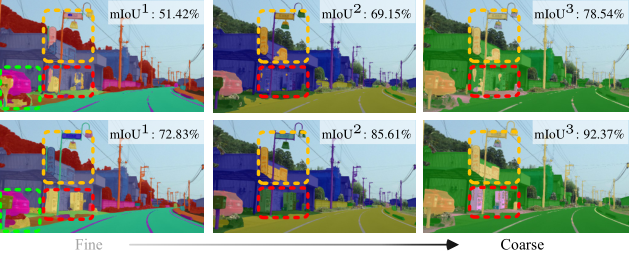
This figure compares effects of (top row) vs. (bottom row). demonstrates higher accuracy for the evaluation metric (mean instersection-over-union).
Figure 4:
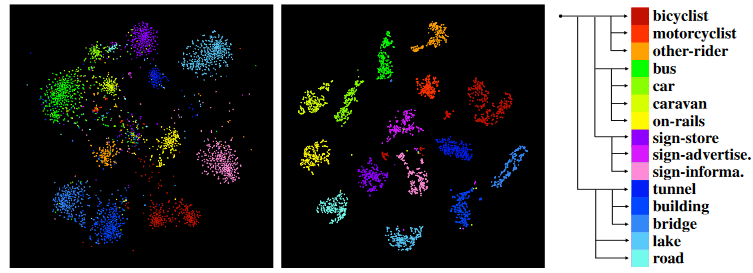
This figure is a visualization of the hierarchal embedding space. The leftmost figure shows this space without (tree-triplet loss) where the rightmost image demonstrates how tree-triplet loss allows the embedding space to embrace the hierarchal semantic structures.
Figure 5:
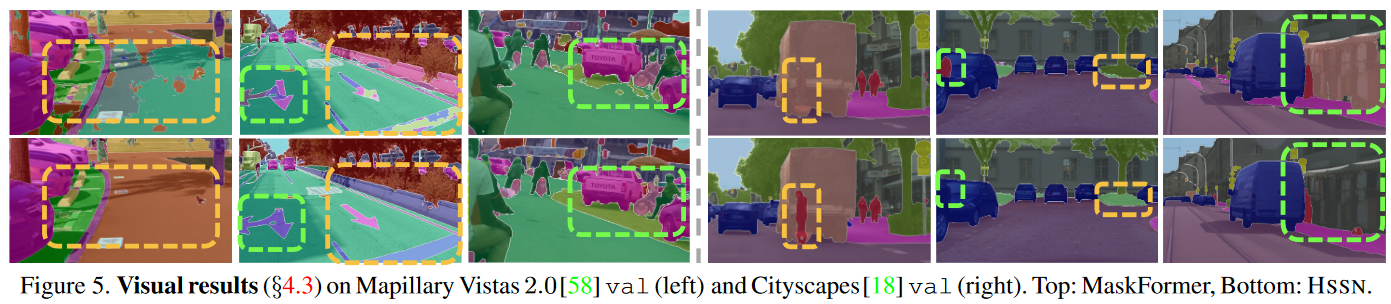
This figure depict representative visual results on four datasets. The top row is a different semantic segmentation network called “MaskFormer” created by FacebookResearch. The purpose of this figure is to compare results between MaskFormer and HSSN. It shows that HSSN yields more precise results than MaskFormer when handling challenging scenes (occlusions, small objects and densely arranged targets, etc).
Figure 6:
This figure compares results between HSSN semantic segmentation and DeepLabV3+ for various scenes from the LIP and Pascal-Person-Part datasets. As apparent, HSSN performs better in each case for the figure given.
What does each table mean?
Table 1:
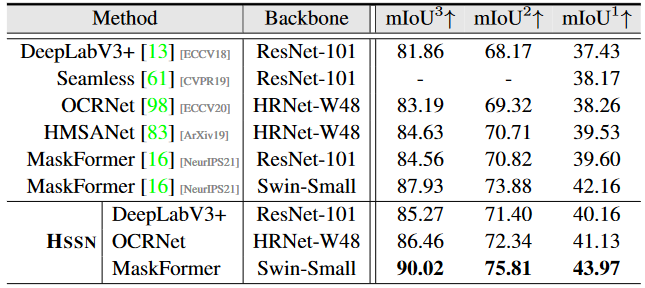Hierarchal semantic segmentation results on the val set of Mapillary Vistas 2.0.
Table 2:
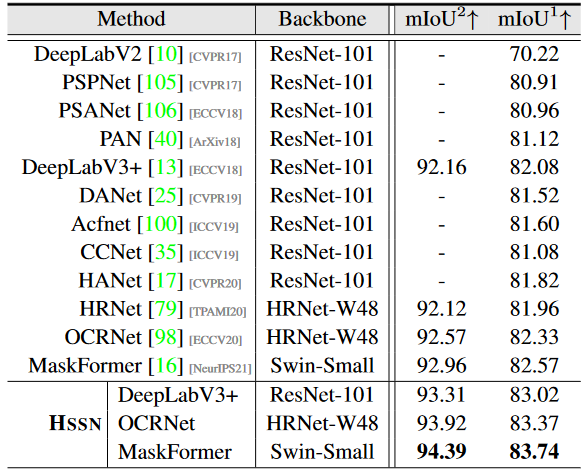Hierarchal semantic segmentation results on val set of Cityscapes.
Table 3:
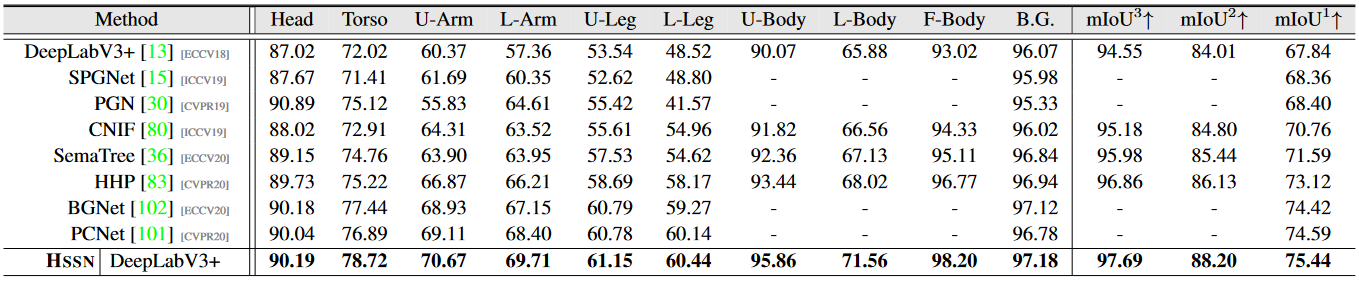Hierarchal human parsing results on PASCAL-Person-Part test. All models using ResNet-101.
Table 4:
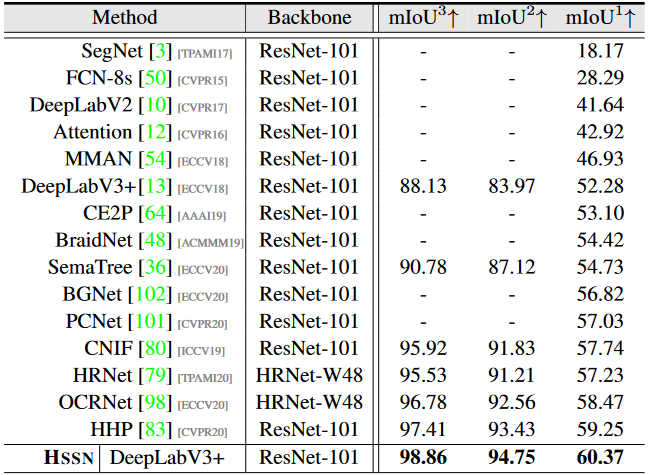Hierarchal human parsing results on LIP val set. Methods such as SegNet are Encoder-Decoder Architectures.
Table 5:
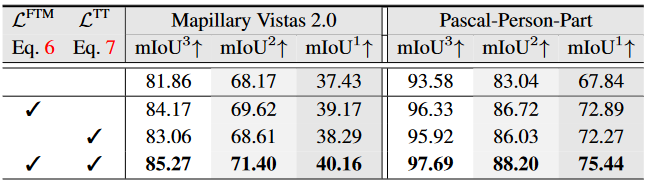Analysis of essential components on Mapillary Vistas 2.0 val and PASCAL-Person-Part test.
Table 6:
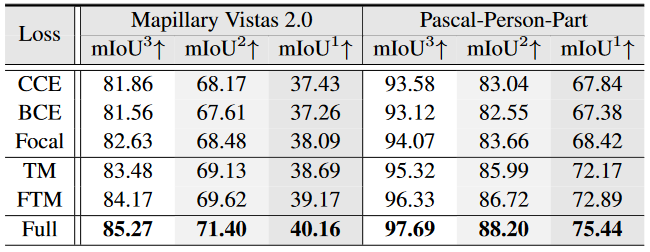Analysis of focal tree-min loss on Mapillary Vistas 2.0 val and PASCAL-Person-Part test.
Table 7:
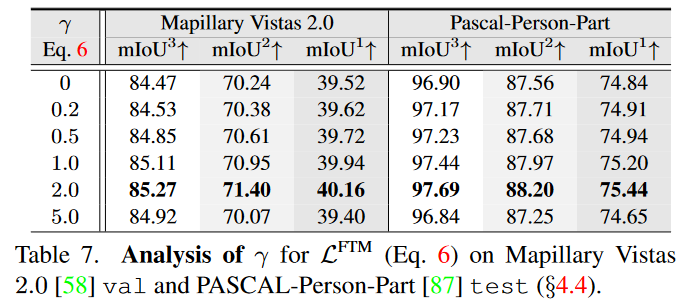(gamma) is a tunable focusing parameter controlling the rate at which easy classes are down-weighted.
Table 8:
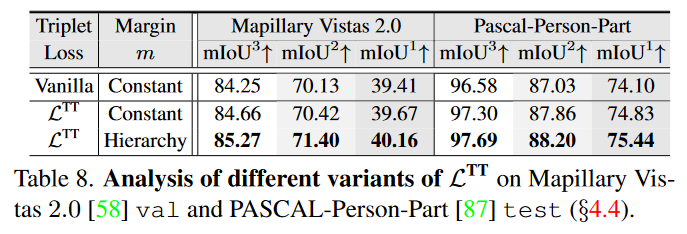
The gains become larger when further applying the hierarchy-induced margin constraint.
Table 9:
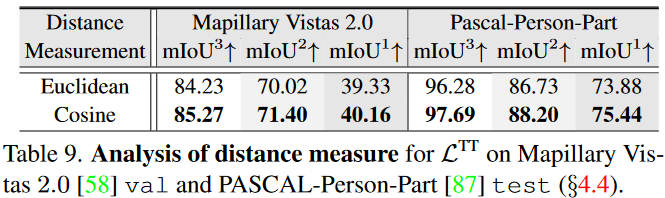
Conclusion:
By exploiting hierarchy properties as optimization criteria, hierarchical violation in the segmentation predictions can be explicitly penalized. HSSN outperforms many existing segmentation models on four famous datasets.
Source:
Deep Hierarchal Semantic Segmentation - Liulei Li, Tianfei Zhou, Wenguan Wang, Jianwu Li , Yi Yang