Anomaly Detection in Machine Learning

Anomaly detection is the identification of rare observations which raise suspicion by nature of differing significantly from the majority of data.

Anomaly detection is useful in cases in which it is easy to collect large quantities of normal examples but where anomalous data is rare and difficult to find.

Anomaly detection algorithms can be unsupervised or supervised, depending on whether labeled data is available or not. Lastly, some applications have used self-supervised learning in which unlabeled data is labeled automatically.

Method 1: Anomaly Detection via Statistical Methods §

To detect anomalies in a quantitative way: first calculate the probability distribution $p(x)$ from the data points. Then when a new example, x, comes in, we compare $p(x)$ with a threshold $r$. If $p(x)<r$, it is considered as an anomaly. This is because normal examples tend to have a large $p(x)$ while anomalous examples tend to have a small $p(x)$.

$\text{*Figure 1: Anomaly detection on two variables.}\ast$

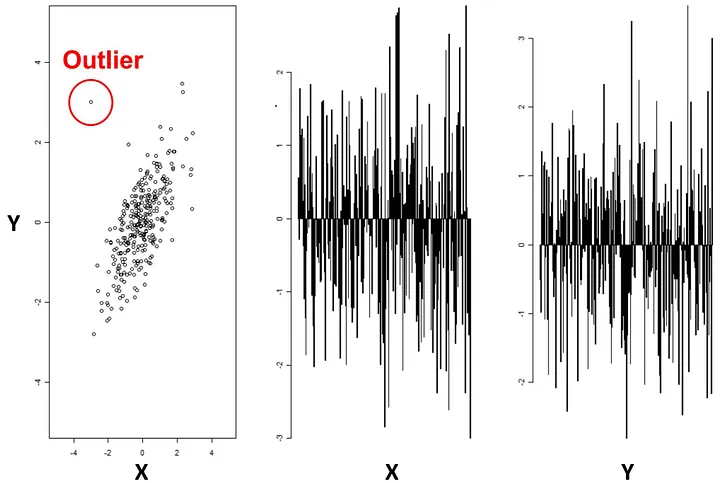
Method 2: Artificial Neural Networks §

Unsupervised Anomaly Detection §

Unsupervised anomaly detection methods include statistical approaches such as Gaussian mixture models, clustering algorithms such as k-means or DBSCAN, and density-based techniques like Local Outlier Factor. These algorithms assume that the majority of the data is normal and attempt to identify the rare instances that deviate significantly from this norm. The potential downside of this paradigm is that unsupervised learning can have high false positive rates and is not suitable for detecting complex anomalies.

Supervised Anomaly Detection §

Supervised anomaly detection methods involve training a model on labeled data that contains both normal and abnormal instances. Common supervised techniques include decision trees, neural networks, and support vector machines. These algorithms use the labeled data to learn the patterns that distinguish normal from abnormal data, and then apply this knowledge to new, unseen data to detect anomalies. Supervised methods can be more accurate than unsupervised methods, especially when the anomalies are complex and difficult to detect. However, it requires labeled data, which may be expensive or time-consuming to obtain.

Figure 3: Examples of potential inputs for Semantic Anomaly Detection

State of the Art: Self-supervised Learning §

Self supervised learning is also applicable to anomaly detection and is a machine learning paradigm in which a model is fed unlabeled data as input and generates data labels automatically, which are then fed to subsequent models as ground truths.

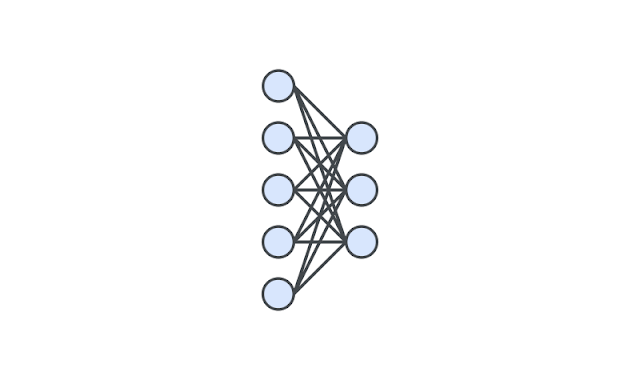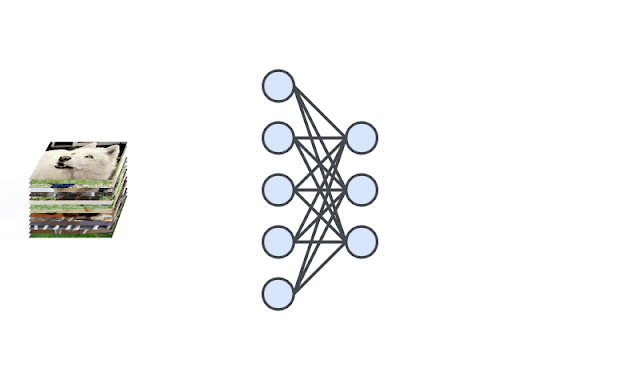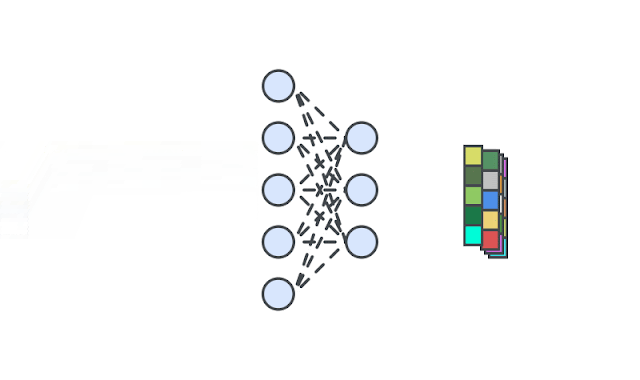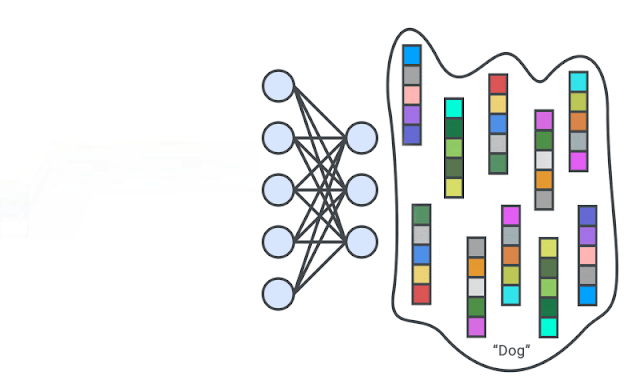
Figure 2: A deep neural network is trained to generate the representations of input images via self-supervision. We then train one-class classifiers on the learned representations.

Autoencoders §

One common approach to self-supervised anomaly detection is to use autoencoders. An autoencoder is a neural network that learns to encode a high-dimensional input into a lower-dimensional representation and then decode it back into the original input. During training, the model tries to minimize the difference between the input and the reconstructed output. Once the model is trained, it can be used to detect anomalies by measuring the difference between the input and the reconstructed output. If the difference exceeds a certain threshold, the input is considered to be anomalous.

Contrastive Learning §

Another approach to self-supervised anomaly detection is to use contrastive learning. Contrastive learning is a self-supervised learning technique that learns to distinguish between similar and dissimilar pairs of data points. In the context of anomaly detection, the model learns to distinguish between normal and abnormal data points by comparing the representations of each data point to the representations of other data points in the same or different classes.

Rotation Prediction §

Rotation prediction refers to a model’s ability to predict the rotated angles of an input image. This method has been widely successful in the field of computer vision & widely adopted for one-class classification research. Rotation prediction may be useful to evaluate classifier accuracy for unlabeled test sets.

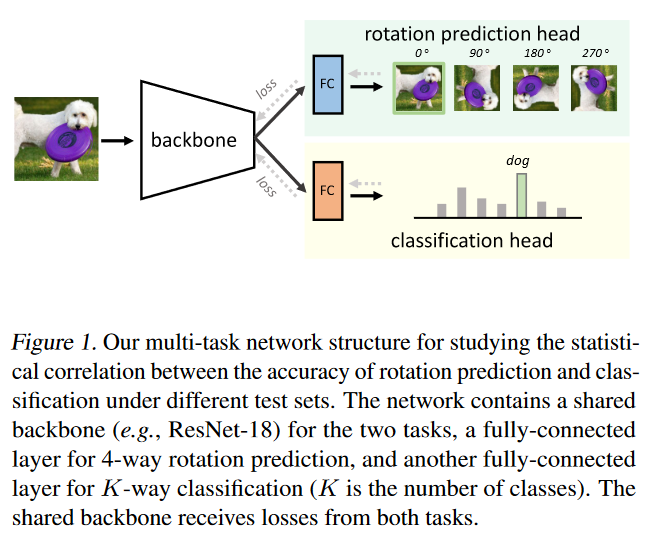
Sources: §

• Discovering Anomalous Data with Self-supervised Learning - Google Research Blog
• How to use machine learning for anomaly detection and condition monitoring - Towards Data Science: Vegard Flovik
• Anomaly Detection for Dummies - Towards Data Science: Susan Li
• What Does Rotation Prediction Tell Us about Classifier Accuracy under Varying Testing Environments? - ArXiv: Weijian Deng, Stephen Gould, Liang Zheng

#evergreen